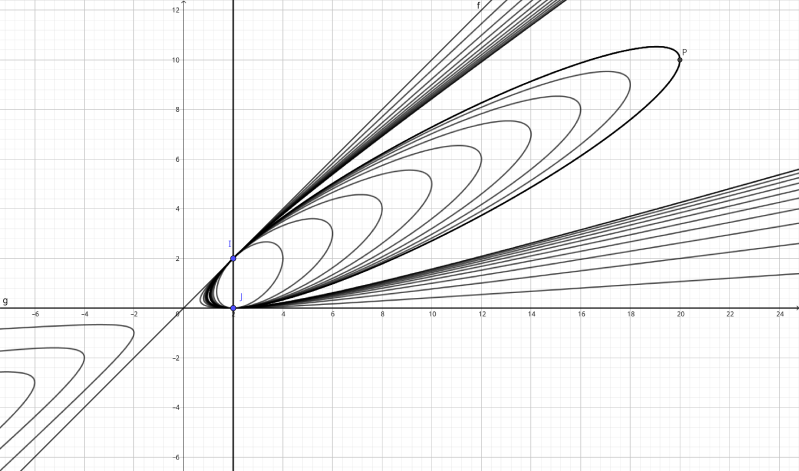
Opgave bij figuur 16.6
Figuur 16.6
Algemene kegelsnede: \begin{equation*} ax^2 + bxy + cy^2 + dx + ey + f = 0 \label{alg-kegel} \end{equation*}Zonder verlies van algemeenheid kunnen we normeren met $a=1$.
We laten de kegelsneden raken aan $l:\; y=0$ in punt $J^\prime(2,0)$ en aan $m:\;y=x$ in punt $I^\prime(2,2)$.
Verder gaat de kegelsnede door een variabel punt $P(2p,p)$. Invullen van de punten geeft de volgende drie vergelijkingen: \begin{alignat}{2} I^\prime(2,2)\quad&\mbox{geeft:}\quad 4+4b+4c+2d+2e+f&=0\\ J^\prime(2,0)\quad&\mbox{geeft:}\quad 4+2d+f&=0\\ P(2p,p)\quad&\mbox{geeft:}\quad 4p^2+2bp^2+cp^2+2dp+ep+f&=0 \end{alignat} Raken aan de lijn $y=x$ geeft: $(1+b+c)x^2+(d+e)x+f=0$, dat is een tweedegraads vergelijking in $x$. De raakvoorwaarde is dat deze vergelijking één oplossing heeft: \begin{equation} (d+e)^2-4f(1+b+c)=0 \end{equation} Raken aan de lijn $y=0$ geeft: \begin{equation} d^2-4f=0 \end{equation} Het stelsel van vijf vergelijkingen heeft als oplossing: $b=\dfrac{8p-4}{p^2}-4$; $c=\dfrac{4-8p}{p^2}+4$; $d=-4$; $e=0$; $f=4$ De schaar van kegelsneden is dus: $$ x^2+\left(\dfrac{8p-4}{p^2}-4\right)xy- \left(\dfrac{8p-4}{p^2}-4\right)y^2-4x+4$$
Veel eleganter is de oplossing van Bernard:
Eén oplossing is de ontaarde ellips $x=2$ (vanaf $y=0$ tot $y=2$)
Deze is te schrijven als: $C=(x-2)^2=0$.
De raaklijnen zijn:
$L_1= x-y = 0$ en $L_2=y= 0$
Met parameter $q$ is de bundel dan: $C+q.L_1\cdot L_2=0$
Oftewel: $(x-2)^2+q(x-y)y=0$,
Uitgewerkt geeft dat: $ x^2 + qxy - qy^2 - 4x + 4 = 0$
Dit is dezelfde oplossing als hierboven met:
$q = \dfrac{8p-4}{p^2}-4$.