Tekening a-084
In de figuur hieronder zien we een bundel kegelsneden door twee reële en twee imaginaire punten. De twee imaginaire punten zijn toegevoegd complex en liggen op een reële rechte lijn, die dus door de kegelsneden niet gesneden wordt, behalve door de ontaarde kegelsnede die bestaat uit een paar van twee snijdende lijnen. De ene daarvan is de de verbindingslijn van de twee reële punten, de andere die van de twee imaginaire punten.

a-084: Pencil of conics having two real points and two
imaginary points in common
Tekenvoorschrift
De punten van kegelsneden zijn te vinden als de snijpunten van twee projectieve, niet perspectieve, lijnenwaaiers. We beginnen dan ook met een lijnenwaaier met constante hoek tussen de lijnen. Deze zal een lijn, die niet tot die waaier behoort, snijden in een puntenreeks in "cirkelmaat".
In de figuur hieronder zie je hoe dat gedaan kan worden.
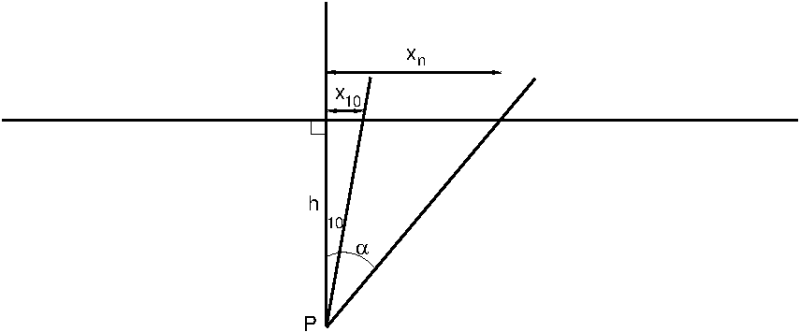
Teken onderaan op een blad papier een horizontale lijn dit wordt de drager van e imaginaire punten. verder komt er ca 20 cm daaronder ($h=20$) een punt $P$. De loodlijn vanuit dat punt op die lijn geeft het midden van de cirkelmaat. Nu kan je vanuit dat punt $P$ een gelijkhoekige ($10^\circ$) waaier tekenen. Maar gemakkelijker en nauwkeuriger is in de figuur te zien dat de afstanden (onafhankelijk van $h$) te berekenen zijn.
$\left.\begin{array}{l} \tan( 10)=\dfrac{x_{10}}{h}\\ \tan (\alpha)=\dfrac{x_n}{h} \end{array}\right\}\Rightarrow x_n=\dfrac{tan(\alpha)}{tan (10)}\cdot x_{10}$.Uitkomsten staan in de tabel hieronder.
$\begin{array}{c||c|c|c|c|c|c|c|c|c|c|c|c|c} \alpha\;(^\circ)&10&20&30&40&50&60&70&80&90\\\hline x \mbox{ (cm)}& 2,55& 5,26& 8,35&12,13&17,23&25,05&39,73&82,01&\infty \end{array}$Op deze schaal heb je dus een groot papier nodig of een of andere handige truc. De afstand $\infty$ bij $\alpha=90^\circ$ betekent dat er bij de waaiers in de reële punten ook een lijn is die evenwijdig loopt aan de drager van de imaginaire punten.
De plaats van de twee vaste reële punten is niet van groot belang. In figuur hierboven zijn ze zò gekozen dat er een fraaie figuur ontstaat.
Als we waaiers tekenen vanuit de reële punten naar de punten van de cirkelmaat dan zijn ze beide lijn-perspectief met de gelijkhoekige waaier. En dus onderling projectief. De snijpunten geven de punten van de bundel van kegelsneden.
In de figuur is $\alpha$ de hoek die er voor zorgt dat er in $G$ en $H$ projectieve waaiers getekend worden. Deze zijn echter niet zichtbaar gemakt.
De hoek $\beta$ (die in de figuur geanimeerd wordt) zorgt ervoor dat telkens een ander stel lijnen, één van waaier $G$ en één van waaier $H$ gesneden worden.
De krommen zijn meetkundige plaatsen van de snijpunten van deze lijnen. Met als variabele de hoek $\alpha$.