Opgave 15.a
In de figuur hieronder zien we een cirkel en een horizontale lijn. De hoogte van deze lijn kan gevarieerd worden met behulp van de schuif a.
Met behulp van de constructie uit paragraaf 15.3 pagina 166 is op die lijn met midden en de amplitude geconstrueerd van het imaginaire puntenpaar dat de cirkel en de lijn y=a gemeenschappelijk hebben.
De uiteinden van het amplitude lijnstuk liggen op een rechthoekige hyperbool (groen), die raakt aan de cirkel.
Hieronder is dezelfde constructie uitgevoerd voor een ellips en voor een hyperbool.
Opgave 15.b
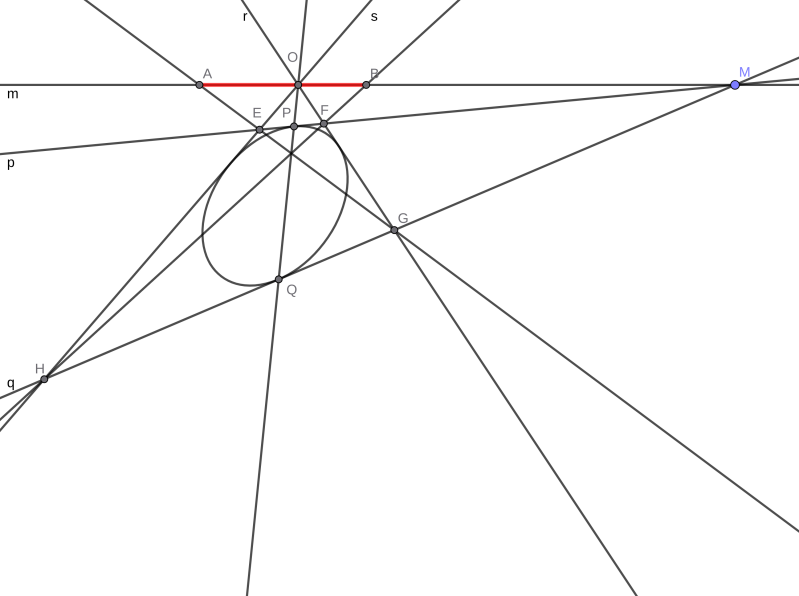

In de linker tekening zie je dat de lijnen die Edwards in figuur 15,4 evenwijdig tekent hier een eindig snijpunt M hebben. De rechter figuur is de duale figuur.
Constructie van de linker figuur
Gegeven de ellips.
Kies een lijn $m$ buiten de ellips, met daarop een punt $M$.
Noem $P$ en $Q$ de snijpunten van $m$ met de ellips.
Dat geeft de raakpunten $P$ en $Q$.
Noem $O$ het snijpunt van $PQ$ met $m$. Dat is het centrum.
Teken vanuit $O$ twee raaklijnen $r$ en $s$ aan de ellips.
Benoem de volgende punten: $E=ps$; $F=pr$; $G=qr$ en $H=qs$.
Nu is $A=EG\wedge m$ en $B=FH\wedge m$ en $AB$ is de gevraagde amplitude.
Constructie van de rechter figuur
Gegeven de ellips.
Kies een punt $M$ binnen de ellips, met daardoorheen een lijn $m$.
Noem $P$ en $Q$ de snijpunten van $m$ met de ellips.
Teken de raaklijnen $r$ in punt $R$ en $s$ in punt $S$.
Verbind het snijpunt van $r$ en $s$ met $M$, dat geeft de centrale straal $o$.
Lijn $o$ snijdt de ellips in $R$ en $S$.
Trek de volgende lijnen: $e=PS$; $f=PR$; $g=QR$ en $h=QS$.
Nu zijn $a=eg\vee M$ en $b=fh\vee M$ de lijnen die de amplitudehoek aangeven.
Een concreet euclidisch geval
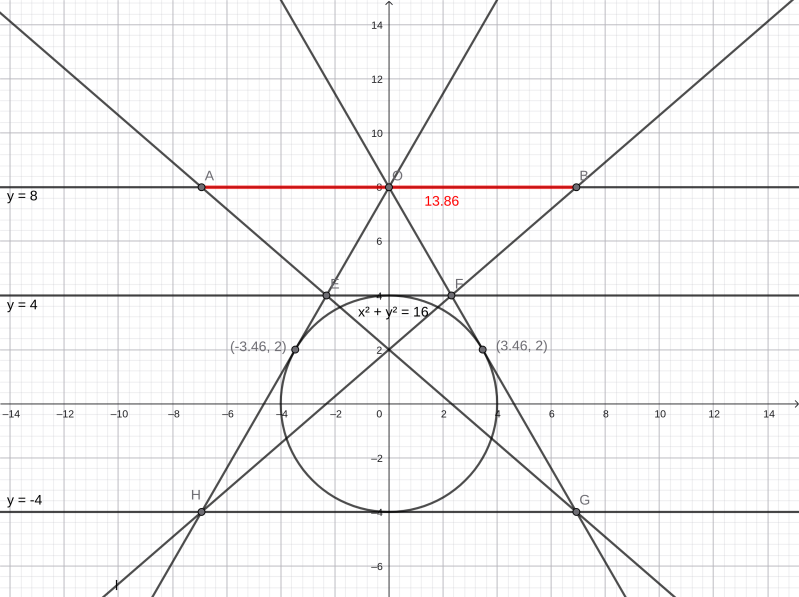
Gegeven de cirkel $x^2+y^2=16$ en de lijn $y=8$.
Bereken met de constructie van figuur LE-15-4 de amplitude van het imaginaire puntenpaar.
$O=(0,8)$, de poollijn $o$ van $O$ is $y=2$,
dat geeft raaklijnen: $r:\; y=-\sqrt{3}x+8$ en $s:\; y=\sqrt{3}x+8$.
Snijden met $p:\; y=4$ en $q:\; y=-4$ geeft de punten:
$E(-\frac{4}{3}\sqrt{3},4)$; $\;F(\frac{4}{3}\sqrt{3},4)$; $\;G(-4\sqrt{3},-4)$; $\;H(4\sqrt{3},-4)$.
De lijn $HF:\; y=\frac{1}{2}\sqrt{3}x+2$ snijden met $m:\; y=8$ geeft: $x_A=4\sqrt{3}$.
Analoog vinden we $x_B=-4\sqrt{3}$
Zodat de amplitude gelijk is aan $8\sqrt{3}$
Snijden van de cirkel $x^2+y^2=16$ met de lijn $y=8$ geeft direct snijpunten bij $x=\pm4\sqrt{3}$, dat geeft dus dezelfde amplitude.
Een concreet euclidisch geval
Gegeven de cirkel $x^2+y^2=16$ en de lijn $y=8$.
Bereken met de constructie van figuur LE-15-4 de amplitude van het imaginaire puntenpaar.
$O=(0,8)$, de poollijn $o$ van $O$ is $y=2$,
dat geeft raaklijnen: $r:\; y=-\sqrt{3}x+8$ en $s:\; y=\sqrt{3}x+8$.
Snijden met $p:\; y=4$ en $q:\; y=-4$ geeft de punten:
$E(-\frac{4}{3}\sqrt{3},4)$; $\;F(\frac{4}{3}\sqrt{3},4)$; $\;G(-4\sqrt{3},-4)$; $\;H(4\sqrt{3},-4)$.
De lijn $HF:\; y=\frac{1}{2}\sqrt{3}x+2$ snijden met $m:\; y=8$ geeft: $x_A=4\sqrt{3}$.
Analoog vinden we $x_B=-4\sqrt{3}$
Zodat de amplitude gelijk is aan $8\sqrt{3}$
Snijden van de cirkel $x^2+y^2=16$ met de lijn $y=8$ geeft direct snijpunten bij $x=\pm4\sqrt{3}$, dat geeft dus dezelfde amplitude.
Opgave 15.c1
In elk punt van de cirkel staat de straal loodrecht op de raaklijn.
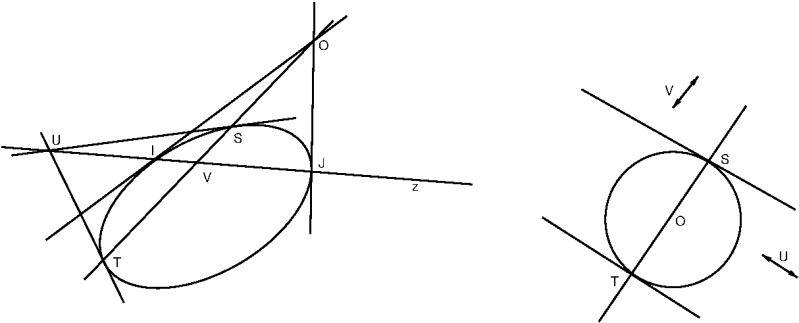
De ellips snijdt de absolute lijn $z$ in $I$ en $J$. Het is dus een cirkel.
Met twee raaklijnen aan de cirkel vinden we $O$, dat is de pool van de absolute lijn $z$, en dus het middelpunt van de cirkel.$OST$ is een middellijn. Met raaklijnen in $S$ en $T$ vinden we de pool $U$ van deze lijn.
$V$ is het snijpunt van $ST$ en $z$. De driehoek $OUV$ is een pooldriehoek. Dus $H(UV\;:\;IJ)$ en dus, perspectief vanuit $T$: $H(TU\;TV\;:\;TI\;J)$.
Dus de raaklijn $TU$ "staat loodrecht op" de middellijn $ST$.$\square$Opgave 15.c2
Omtrekshoeken op een sector zijn gelijk.
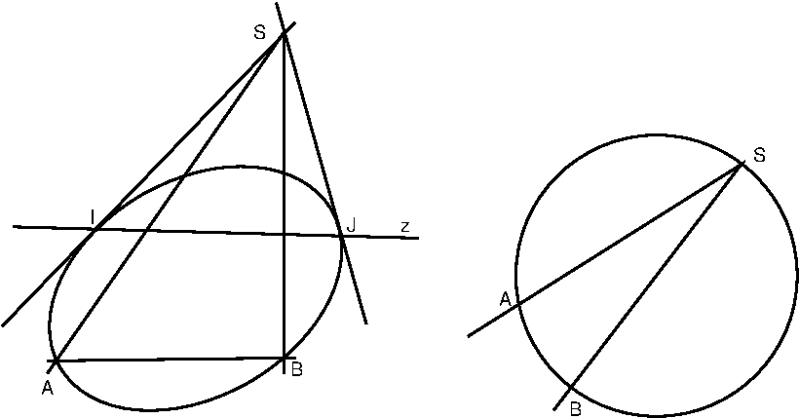
Hoeken zijn gelijk als de dubbelverhouding van hun twee benen en de twee isotrope richtingen gelijk zijn.
Zie de cirkel als een kegelsnede die $I$ en $J$ bevat en waarvan een segment begrensd wordt door punten $A$ en $B$.Trek van een willekeurig punt $S$ op op die kegelsnede de lijnen $SA$, $SB$, $SI$ en $SJ$.
De dubbelverhouding $SABIJ$ in de lijnenwaaier om $S$is onafhankelijk van de plaats van $S$ op de kegelsnede, want $ABIJ$ liggen op een tweede orde puntenreeks op de kegelsnede.
Dus is de hoek $ASB$ voor elke $S$ op de kegelsnede -- die cirkel, omdat $I$ en $J$ erop liggen -- gelijk. $\square$
Opgave 15.c3
De lijn vanuit het midden van een cirkel naar het midden van een koorde staat loodrecht op die koorde.
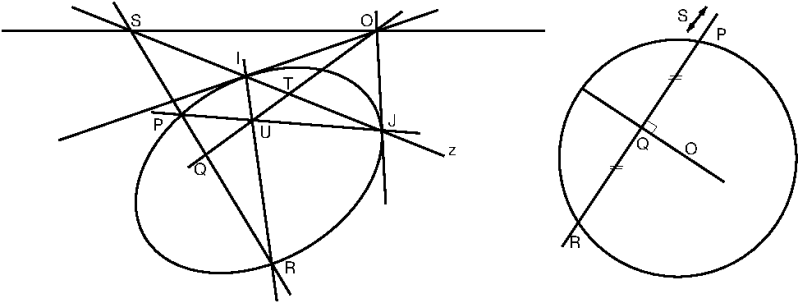
De ellips snijdt de absolute lijn $z$ in $I$ en $J$. Het is dus een cirkel. Met twee raaklijnen in resp $I$ en $J$ aan de cirkel vinden we $O$, het middelpunt van de cirkel.
We tekenen twee ``evenwijdige`` koorden $IJ$ en $PR$, deze snijden elkaar in $S$ op de oneindig verre lijn van het vlak $z$.
We noemen $U= JP\wedge IR$. Teken nu de middellijn $OQ$ door $U$. Deze snijdt $PR$ in $Q$. $OQ$ is poollijn van $S$,en daarom geldt: $H(SQ\;:\;PR)$.
$S$ ligt op $z=l_\infty$ dus $Q$ is het ``midden`` van $PR$.
Tegelijkertijd geldt: $H(ST\;IJ)$ en dus ook: $H(OS\;OT\;:\;OI\; OJ)$. Dus staat $OS$ ''loodrecht'' op $OT$.
$RS$ is ``evenwijdig`` aan $OS$ (snijpunt op $z$) dus $OS$ staat ook ``loodrecht``op $RS$.$\square$
Opgave 15.c4
De hoogtelijn vanuit de top van een gelijkbenige driehoek deelt de basis door midden.
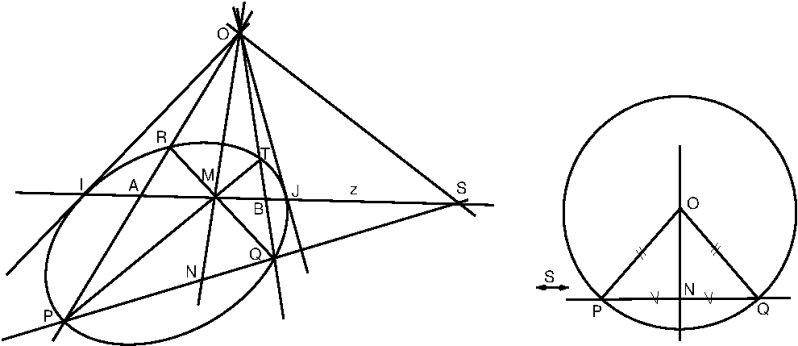
Hier weer een cirkel met middelpunt $O$.
Volgens punt 7 op pagina 171, geldt dat $OP=OQ$, de driehoek $\triangle OPQ$ is gelijkbenig.$PQTR$ is weer een volledige vierhoek. Uit $H(IJ\;:\;MS)$ volgt dat $OM$ ``loodrecht`` staat op $OS$ en omdat $OS$ ``evenwijdig loopt`` aan $PQ$ (snijpunt op $z=l_\infty$) staat $ON$ ``loodrecht op $PQ$.
Met $H(AB\;:\;MS)$ en $AMBS\stackrel{O}{\doublebarwedge}PNQS$ krijgen we $H(PQ:NS)$; dus $N$ is het ``midden`` van $PQ$. $\square$